Lekcja: Objętość brył – prostopadłościan, walec, kula

1. Co to jest objętość?

Objętość bryły to miara, która mówi, ile miejsca zajmuje bryła w przestrzeni.

Objętość podajemy w jednostkach sześciennych, np. $\text{cm}^3$, $\text{m}^3$.

—

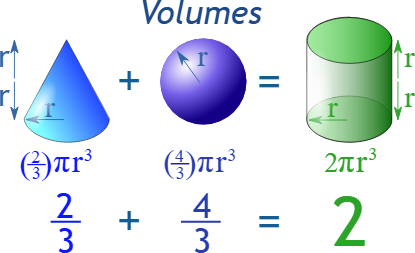
2. Prostopadłościan

Prostopadłościan to bryła, która ma 6 ścian w kształcie prostokątów.

Jeśli oznaczymy:

* długość = $a$,

* szerokość = $b$,

* wysokość = $h$,

to jego objętość obliczamy ze wzoru:

$$V = a \cdot b \cdot h$$

Przykład

Pudełko ma wymiary: $a = 3 \, \text{cm}$, $b = 4 \, \text{cm}$, $h = 5 \, \text{cm}$.

$$V = 3 \cdot 4 \cdot 5 = 60 \, \text{cm}^3$$

—

3. Walec

Walec ma podstawę w kształcie koła i wysokość $h$.

Promień podstawy oznaczamy jako $r$.

Objętość walca obliczamy ze wzoru:

$$V = \pi r^2 h$$

Przykład

Walec ma promień $r = 2 \, \text{cm}$ i wysokość $h = 10 \, \text{cm}$.

$$V = \pi \cdot 2^2 \cdot 10 = 40\pi \, \text{cm}^3$$

—

4. Kula

Kula to bryła, w której wszystkie punkty znajdują się w tej samej odległości $r$ od środka.

Objętość kuli obliczamy ze wzoru:

$$V = \frac{4}{3} \pi r^3$$

Przykład

Kula ma promień $r = 3 \, \text{cm}$.

$$V = \frac{4}{3} \pi \cdot 3^3 = \frac{4}{3} \pi \cdot 27 = 36\pi \, \text{cm}^3$$

—

5. Podsumowanie

* Prostopadłościan: $\, V = a \cdot b \cdot h$

* Walec: $\, V = \pi r^2 h$

* Kula: $\, V = \tfrac{4}{3} \pi r^3$

—

6. Ćwiczenia – karta pracy

• Oblicz objętość prostopadłościanu o wymiarach: $a = 5 \, \text{cm}$, $b = 2 \, \text{cm}$, $h = 10 \, \text{cm}$.
• Oblicz objętość walca o promieniu $r = 4 \, \text{cm}$ i wysokości $h = 6 \, \text{cm}$.
• Oblicz objętość kuli o promieniu $r = 5 \, \text{cm}$.
• W zeszycie narysuj każdy z wymienionych typów brył i podpisz ich wymiary.